تكنلوجيا النمذجة الهندسية

مقدمة:

تعتمد البرامج الإنشائية على نظرية العناصر المحدودة والتي تعتمد على تقسيم العنصر المدروس إلى عدد من العناصر المحدودة بعقد و من ثم حساب الانتقالات في هذه العقد و تجميع الانتقالات للعنصر المدروس و منه معرفة الإجهادات و القوى المطلوبة حسب نظرية المرونة .

لذلك فإن زمن التحليل يعتمد و بشكل أساسي على عدد هذه العناصر  (أي عدد درجات الحرية)

حيث أن زمن التحليل يتناسب مع  (N(dof,a  حيث  يمثل dof عدد درجات الحرية الكلي في النموذج المدروس و a عامل يساوي  يعتمد على شكل العنصر المحدود وعلى شكل مصفوفة القساوة , فمن واجب المحلل العمل على التقليل من استخدام موارد الحاسب و ذلك عبر مراعاة مايلي :

1 – استخدام أقل عدد ممكن من درجات الحرية.

2 – استخدام التقسيم الخشن, و تنعيم التقسيم في أماكن تركز الإجهادات (حول الفتحات مثلا).

3 – معرفة الشروط الحدية  و طريقة تمثيلها .

4 – معرفة الحمولات بشكل جيد و طريقة نقلها إلى النموذج الحاسوبي.

من أجل التقليل من استخدام موارد الحاسب يفضل إن أمكن استخدام خاصية التناظر .

التناظر (SYMMETRY) :

لا تخلو مسألة إنشائية من التناظر حيث نصادف التناظر في كثير من النماذج منها الخزانات و الشبكيات والمنشات المطمورة , فمثلا يتكون برج إيفل من أكثر من 100,000   عنصر و بما أنه متناظر حول المستويين XZ,YZ   لذلك يكفي نمذجة ربع البرج باستخدام عدد من القواعد و بالتالي يقل عدد العناصر إلى  25,000  عنصر  أي أن عدد درجات الحرية في المنشأ سيقل إلى الربع و باستخدام علاقة الزمن بعدد درجات الحرية و بفرض  نجد أن زمن التحليل سيقل بمقدار 64  مرة , ولكن كيف نستفيد من هذا التناظر من أجل التقليل من زمن التحليل أو ما يسمى الكلفة ؟

بداية يجب أن يكون المنشأ متناظر من حيث الأبعاد الهندسية و المواد و الحمولات و تسمى حالة التناظر هذه symmetric case أما عندما تكون الحمولات متعاكسة (متناظرة من حيث الموقع و الشدة و متعاكسة بالإتجاه ) عندها تسمى هذه الحالة anti-symmetric

فلنمذجة منشأ  ما نكتفي بنمذجة الجزء المتناظر منه حول مستو ما لكن لدينا مشكلة الشروط الحدية للجزء المدروس في منطقة اتصاله مع المنشأ الأصلي و من أجل ذلك نتبع الشروط التالية :

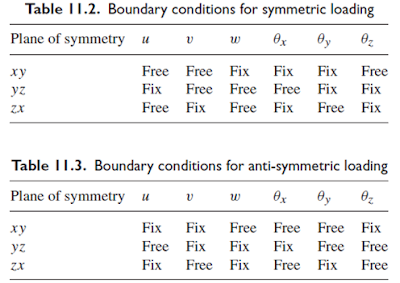
في المنشآت symmetric نتبع الشروط الحدية التالية :

1 – لا يوجد مكونات انتقالات عمودية على مستو التناظر

2 – لا يوجد دورانات منتقلة متعلقة بالمحور الموازي لمستو التناظر

أما في المنشآت anti-symmetric نتبع الشروط الحدية التالية :

1 – لا يوجد مكونات انتقالات موازية لمستو التناظر

2 ---_ لا يوجد دورانات منتقلة متعلقة بالمحور العمودي  لمستو التناظر

ويمكن صياغة ما سبق بالجدول التالي :

و كمثال لما سبق نعتبر الجائز البسيط التالي :

 

نمذجة نصف الجائز  باعتماد الشروط الحدية للمنشآت من النوع symmetric

 

نمذجة نصف الجائز  باعتماد الشروط الحدية للمنشآت من النوع anti-symmetric

و يمكن استخدام خاصية التناظر من أجل تمثيل أنماط الإهتزاز الديناميكية كما في الشكل :

  

التناظر المحوري Axial Symmetry  :

من المسائل الهامة جدا في مجال الهندسة الإنشائية مسائل التناظر المحوري فنصادف هذا التناظر في العديد من المسائل منها الأنابيب و الخزانات و تمثيل التربة و في الكثير من المنشآت الفراغية حيث ندعو  المنشأ متناظر محوريا إذا أمكن توليده عبر دوران عنصر أو مستو  ما حول محور رئسي لهذا المنشأ و بذلك نجد أن المسألة ثلاثية الأبعاد تتحول إلى مسألة ثناثية الأبعاد و المسألة الثناثية تتحول إلى مسألة أحادية , علما أننا نعتبر المسألة من النوع Axisymmetric  إذا كان التناظر حول محور ما هو تناظر كامل من حيث المقطع و الحمولات و المواد .

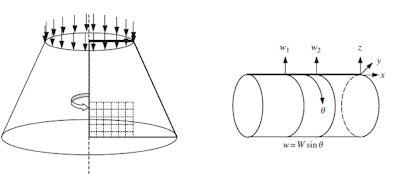
ففي الشكل أعلاه يكفي نمذجة عنصر خطي واحد لتوليد الإسطوانة و نمذجة مستو واحد لتوليد جذع المخروط , و يجب ملاحظة أن العنصر المحدود المستخدم في نمذجة عناصر axisymmetric elements تسمى عناصر  Asolid element .

من البرامج التي تعالج مسائل التناظر المحوري برنامج Sap2000 برنامج  حيث يعتمد البرنامج على عنصر محدود مكون من 3 أو  4   عقد كما في الشكل :

و سنشرح فيما يلي أساسيات  دراسة هذه العناصر :

نعتمد للدراسة الجملة الإحداثية القطبية حيث نستبدل المحاور الإحداثية X,Y,Z  بالمحاور R,θ,Z  بالترتيب و ندرس العنصر الجزئي الموضح في الشكل التالي :

و تكون الإجهادات المتولدة في هذا النوع من العناصر هي :

حيث ترتبط الإجهادات بالتشوهات عبر مصفوفة التشكيل :

 

و  ترتبط التشوهات بالإنتقالات بالعلاقات التالية :

 

و نورد فيما يلي مثال لاستخدام التناضر المحوري :

المطلوب تمثيل ضغط أساس على تربة باستخدام عناصر Asolid في برنامج Sap 2000

خطوات الحل :

1 – نأخذ شريحة من الوسط المدروس بحيث يتولد الوسط بدوران هذه الشرحة حول المحور Z

2 - نقوم بنمذجتها على برنامج SAP  باستخدام عنصر ASOLID  و بإعطاء زاوية سماكة قدرها 1 درجة فنكون بذلك مثلنا الوسط بشكل ثلاثي الأبعاد .